##----- Méthode de Malo modifiée pour la détection de points noirs de collisions -----##
library(rgdal)
library(secrlinear)
sec <- 100 #nb de collisions mesuré tout les 'sec' m = taille de section
int <- 2 #distance d'analyse = (sec * 2int) + sec = 500m ici
Nrep <- 1000 #Nombre de simulations
##Importation des données au format shapefile ; route = rte ; collisions = pts
rte <- readOGR("./Donnees","route_ploermel")
pts <- readOGR("./Données","patr_ploermel")
Net <- read.linearmask(data=rte)
distance <- networkdistance (Net[1,], pts@coords, Net)
pts@data[,"NumKM"]<-t(floor(distance/sec))[,1]
##Réalisation des Nrep simulations de poisson
lgrte <- networkdistance(Net[1,], Net[nrow(Net),], Net)
rand <- list()
Lambda <- array(NA, list(floor(lgrte/sec)+1, Nrep), list(0:floor(lgrte/sec),1:Nrep))
for(i in 1:Nrep){
rand[[i]] <- sim.linearpopn(Net, N=length(pts), Ndist = c('poisson','fixed'))
distanceR <- networkdistance(Net[1,], rand[[i]], Net)
rand[[i]][,"NumKM"]<-t(floor(distanceR/sec))[,1]
NbObs_km_R <- tapply(rand[[i]][,"NumKM"], rand[[i]][,"NumKM"], length)
Lambda[,i] <- NbObs_km_R[match(rownames(Lambda),names(NbObs_km_R))]
}
##Calcul du nombre de collisions par 500m tous les 100m pour chaque simulation
Lambda[is.na(Lambda)]<-0
Lambdat <- t(Lambda)
XR <- array(NA, list(Nrep, floor(lgrte/sec)+1), list(1:Nrep, 0:floor(lgrte/sec)))
for(j in 1:Nrep){
for(i in 1:ncol(Lambdat)-2){
XR[j,i] <- sum(Lambdat[j,abs(i-int):(i+int)])
}
}
##Calcul du nombre moyen de collisions dans 500m, calcul issu des simulations
LambdaMoy <- apply(t(XR), 1, mean, na.rm=T)
LambdaMoyMoy <- mean(LambdaMoy)
##Calcul du seuil
Seuil <- qpois(.975, lambda=LambdaMoyMoy)
##Calcul du nombre de collisions par 500m tous les 100m pour les données d’intérêt
NbObs_km <- tapply(pts@data[,"NumKM"], pts@data[,"NumKM"], length)
X <- NbObs_km[match(rownames(Lambda),names(NbObs_km))] ; X[is.na(X)] <- 0; names(X) <- rownames(Lambda)
X1 <- X
for(i in 1:length(X)-2){
X1[i] <- sum(X[abs(i-int):(i+int)])
}
##Récupération des collisions comprises dans les PN (Nombre de collisions > Seuil)
DataSupSeuil <- pts@data[pts@data$NumKM %in% as.integer(names(X1[X1>Seuil])),]
##Récupération des sections de route des PN (Nombre de collisions > Seuil)
distanceRte <- networkdistance (Net[1,], Net, Net)
Net[,"NumKM"] <- t(floor(distanceRte/sec))[,1]
PtsSupSeuil <- as.data.frame(Net[Net$NumKM %in% as.integer(names(X1[X1>Seuil])),])
##Exportation des résultats au format shapefile
coordinates(PtsSupSeuil) <- ~x+y
proj4string(PtsSupSeuil) <- CRS("+proj=lcc +lat_1=49 +lat_2=44 +lat_0=46.5 +lon_0=3 +x_0=700000 +y_0=6600000
+ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs")
writeOGR(PtsSupSeuil, dsn = "./Documents/Resultats", layer = "Resultat_Malo", driver = "ESRI Shapefile")
#Malo, J.E.; Suárez, F.; Diez, A. 2004. Can we mitigate animal–vehicle accidents using predictive models? Journal of Applied Ecology 41: 701–710.
##----- Simulations de Kernel Density Estimation pour la détection de points noirs de collisions -----##
library(spatstat)
library(rgdal)
library(maptools)
nsim <- 1000
sigma <- 500
##Importation des données au format shapefile ; route = rte ; collisions = pts
rte <- readOGR("./Donnees","route_pleslin")
pts <- readOGR("./Donnée","patr_pleslin")
##Extraction des coordonnées au format ‘ppp’ et conversion de la route au format ‘linnet’
pts_PPP <- as.ppp(pts@coords,owin(c(min(pts@coords[,1]),max(pts@coords[,1])),c(min(pts@coords[,2]),max(pts@coords[,2]))))
rteLinnet <- as.linnet(rte)
##Création du lpp (i.e. route + collisions)
ptsrte <- lpp(pts_PPP,rteLinnet)
unitname(ptsrte) <- c("metre","metres")
##Calcul du Kernel Density Estimation
kde <- density.lpp(ptsrte, sigma=sigma)
value <- attr(kde, "df")
##Réalisation des simulations de Poisson pour la détermination de la valeur seuil
lambda <- ptsrte$data[[2]]/sum(lengths.psp(as.psp(rteLinnet))) # = Nombre de collisions par km
sims <- rpoislpp(L = rteLinnet, lambda = lambda, nsim = nsim) #Simulations de poisson
simKDE <- lapply(X = sims, FUN = density.lpp, sigma = sigma) #Application du KDE aux simulations
simdf <- lapply(X = simKDE, FUN = attr, which = "df")
simvalue <- lapply(X = simdf, FUN = subset, select = "values") #Extraction des résultats
dfvalue <- data.frame(V1=do.call(c,lapply(simvalue, function(x) mean(x$values, na.rm=T)))) #Calcul pour chaque simulation de la valeur moyenne du KDE
seuil <- quantile(dfvalue$V1, .95)#Détermination du 95e centile du KDE moyen de chaque simulation
valueseuil <- value[value$values > seuil,]#Selection des données supérieur au seuil
##Exportation des résultats au format shapefile
coordinates(valueseuil) <- ~x+y
proj4string(valueseuil) <- CRS("+proj=lcc +lat_1=49 +lat_2=44 +lat_0=46.5 +lon_0=3 +x_0=700000 +y_0=6600000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs")
writeOGR(valueseuil, dsn = "./Documents/Resultats", layer = "Resultat_KDE", driver = "ESRI Shapefile")
#Baddeley, A.; Turner, R. 2005. spatstat : An R Package for Analyzing Spatial Point Patterns. Journal of Statistical Software 12: 1–42.
#Bíl, M.; Andrášik, R.; Janoška, Z. 2013. Identification of hazardous road locations of traffic accidents by means of kernel density estimation and cluster significance evaluation. Accident Analysis & Prevention 55: 265–273.
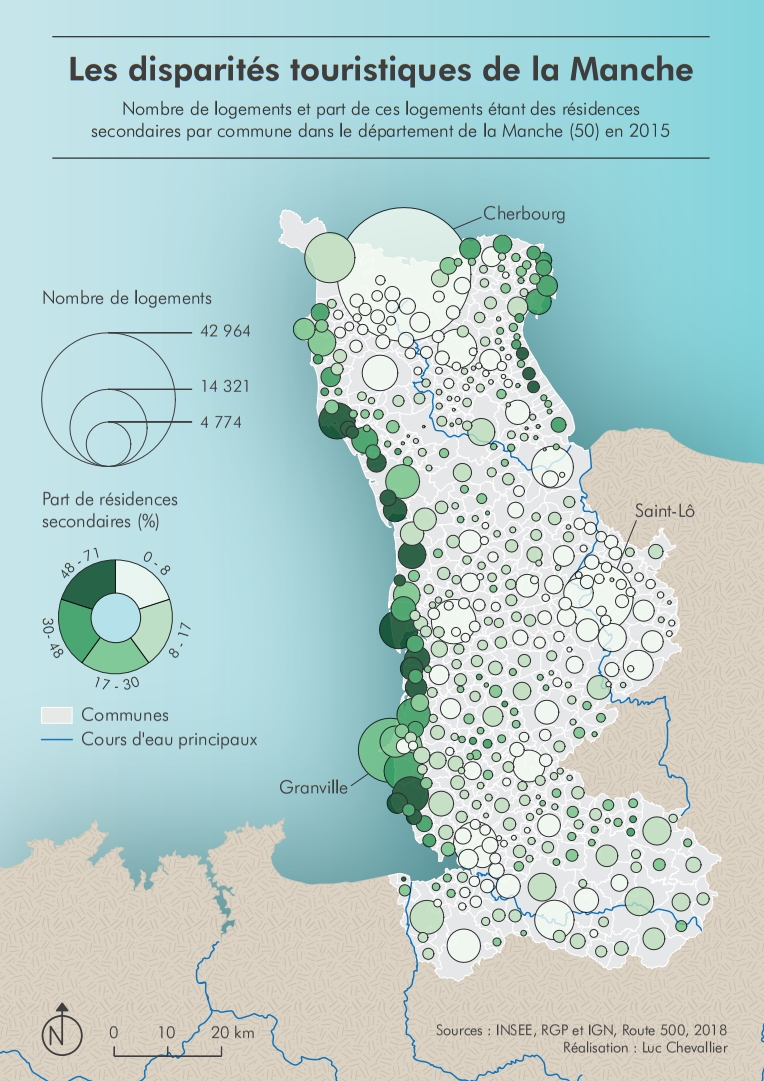
 Quelques réalisations graphiques
Quelques réalisations graphiques Quelques analyses statistiques développées sous R
Quelques analyses statistiques développées sous R